作者 ny_123457

注：如果图片太小看不太清，hcz建议可以点击图片放大。

Part 1.树状数组

首先这个东西真的巨好用，它是利用数的二进制特征进行检索的一种树状结构，（虽然它模版绿），代码很短，仅需三个函数就可以实现单点修改，区间查询（区间求和），效率也很高。

接下来介绍树状数组是个什么玩意。

它都叫树状数组了，肯定要搞一棵树啊，假设我们有一个数列，然后问你一堆诸如求一个区间的最值或求区间和的问题，数据范围还很大，请问你怎么办？暴力怼上去啊，能骗几分骗几分。（考场上实在没办法了才打暴力。）

这时候就可以写树状数组了（其实针对这个题也可以写后面才讲的线段树，但是线段树码量太大了，还是建议写树状数组），我们先设定有两个数组，\(A\) 数组和 \(C\) 数组，其中 \(A\) 数组为我们输入的数组，\(C\) 数组需要我们自行计算。

\(C\) 数组的计算如下：
\(C_1=A_1\)
\(C_2=A_1+A_2\)
\(C_3=A_3\)
\(C_4=A_1+A_2+A_3+A_4\)
\(C_5=A_5\)
\(C_6=A_5+A_6\)
\(C_7=A_7\)
\(C_8=A_1+A_2+A_3+ \cdots +A_8\)
\(\cdots\)

等等，它不是一种用二进制特征进行检索的树状数据结构吗？这跟二进制有什么联系？（阅读本文时建议先思考这个问题在往下读）

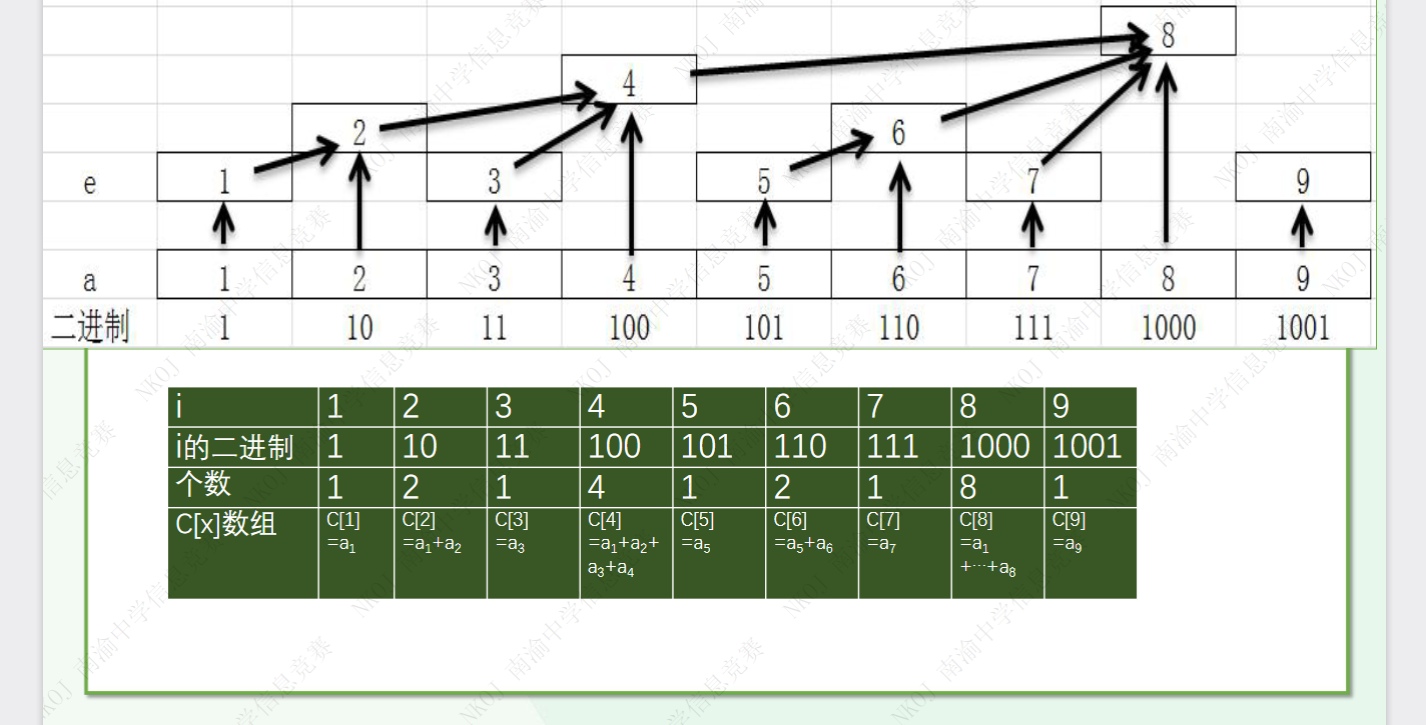
114514.PNG

把 \(C\) 数组转化为递推表达式就是 \(C_i=A_{2^k+1}+ \cdots +A_i\)。其中 \(k\) 为 \(i\) 对应的二进制数末尾 \(0\) 的个数，\(i\) 从 \(1\) 开始计算，但是问题又来了，知道 \(i\) 怎么求 \(2^k\)？我们 C++ 代码中的与运算能够很好的解决这个问题，将答案写入代码中就是 i&(-i)（不了解位运算的建议去翻别人的博客学习一下）。

于是，我们的第一个函数就诞生了：

1
2
3
int lowbit(int x){
    return x&(-x);
}

然后我们再来思考关于求和的问题，当我们求 \(A_1+A_2+ \cdots +A_x\) 的之和时，\(C_x\) 如果包含的不一定是 \(1\) 到 \(x\) 的全部和（比如 \(C_6=A_5+A_6\)） 就需要再找一个 \(C_k\)（显然 \(k<x\)）累加起来，这个 \(k\) 我们称之为 \(x\) 的前驱，例如:

\(A_1+A_2+ \cdots +A_6=C_6+C_4\)
\(A_1+A_2+ \cdots +A_7=C_7+C_6+C_4\)

前驱的编号：比自己小的，最近的，最末连续 \(0\) 比自己多的数（在二进制下）。

所以设 \(x\) 的前驱为 \(k\)，则 k=x-lowbit(x)，相当于 \(x\) 减掉了自己最右边的 \(1\)。

所以，我们的第二个用于求和的函数诞生了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int getsum(int x){
	int sum=0;
	for(int k=x;k>0;k-=lowbit(k))sum+=c[k];
	return sum;
}
```   
这个只能用于求从 $1$ 到 $x$ 项的和，如果要求区间和，假设是区间 $[x,y]$，则这个区间的区间和就为 ```getsum(y)-getsum(x-1)```。（减一是因为 $A_x$ 也是算入这个区间的。）

然后就是剩下的单点修改了，还是前面放的那个图，如果修改了某个 $A_i$ 那么所有跟这个 $A_i$ 相关的 $C_i$ 就也全部需要修改，翻译成人话就是更改从该叶子节点到根节点路径上的所有 $C_i$。这里的父亲节点就是比自己大的，最近的，二进制下末尾 $0$ 的数量最多的数，所以 $x$ 节点的父亲节点的编号就是 ```x+lowbit(x)```。

单点修改函数如下：  

```cpp
void modify(int x,int y){
    for(int i=x;i<=n;i+=lowbit(i))c[i]+=y;
}

最后一看，我滴妈呀，时间复杂度仅为 \(O(\log n)\)，所以一般情况下能写树状数组就写树状数组（单纯想练习线段树的除外）。

然后恭喜你已学会树状数组的基本操作！

Part 2.线段树

该来的还是来了。这个东西和树状数组很像，但是它比树状数组多支持了个区间修改和区间查询，效率也很高，但有个很无语的缺点：码量太大了，动不动就一百多行的，这也就意味着很难调，考场遇到了如果时间不那么充足就建议直接打个暴力上去，线段树的题暴力分一般会比较高。

线段树是一种特殊的二叉树，它可以将一个线性的序列组织成一个树状结构，从而可以在对数的时间复杂度下访问序列上的任意一个区间并进行维护，在线段树中，每一个节点要么没有子节点，有么就有两个子节点，其中每一个节点记录的都是一个区间和或一个区间的最值，一个父亲节点的值就为它的两个儿子节点的值的合并体，举个例子，如果这个节点的子节点记录的分别是区间 \([1,3]\) 和区间 \([4,5]\) 的和（或最值），它们的父亲节点记录的就是区间 \([1,5]\) 的和（或最值），线段树支持单点修改，区间修改，单点查询，区间查询。

下面的图片所呈现的就是一个合法的线段树：

logo

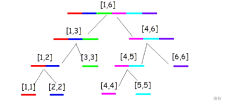
若一个节点的编号为 \(x\)，那么它的子节点的编号就分别为 \(2 \times x\) 与 \(2 \times x +1\)。二叉树常识都知道的吧。

一些线段树的性质：
- 长度为 \(n\) 的序列建的线段树，节点个数为 \(2n-1\)。 - 长度为 \(n\) 的序列建的线段树，树深度为 \(\log(n)\)。 - 线段树需要维护的东西一定具有可合并性。

接下来就可以想想怎么建树了，上文说了，一个节点表示的是一个区间的数据，因此一个节点要至少三个数据，分别是左端点，右端点和区间数据（如果有区间修改这种高级操作那么就还需要一个懒标记，作用后文会提到）由于这是一颗二叉树，而我们输入的是一个序列，因此空间需要开四倍。

接下来就可以写合并和建树的函数了，首先合并的题目给啥合并啥，比如求和的那么当前节点的区间数据即为它两个儿子的区间数据的和，最值即为它两个儿子的区间数据的最值。建树就可以用递归（和 DFS 的思路差不多）进行，一直往下推，如果当前节点的左端点与右端点重合（区间仅为这单独的一个点），那么这个节点的区间数据即为这个单独的点的值，单点建树时间复杂度同样为 \(O(\log(n))\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
struct lilaoshi{
	int l,r,val;
}tree[4*maxn];
void pushup(int p){
	tree[p].val=tree[2*p].val+tree[2*p+1].val;
}//这里以求和为例
void build(int p,int x,int y){
	tree[p].l=x;
	tree[p].r=y;
	if(x==y){
		tree[p].val=a[x];
		return;
	}
	int mid=(x+y)/2;
	build(p<<1,x,mid);
	build(p<<1|1,mid+1,y);
	pushup(p);
}

现在就该考虑单点修改操作了，可以先设一个需要改变的值，然后就是需要改变的数和当前改变的数的编号，然后就是与 build 函数一样的思想，先往下递归，如果这是一个单点区间，那么就直接更改该节点的区间数据，否则就二分下去查找（遍历自己的两个儿子），时间复杂度（单点修改）同样为 \(O(\log(n))\)。

1
2
3
4
5
6
7
8
9
void add(int p,int k,int d){
	if(tree[p].l==tree[p].r){
		tree[p].val+=d;
		return;
	}
	if(k<=tree[p<<1].r)add(p<<1,k,d);
	if(k>=tree[p<<1|1].l)add(p<<1|1,k,d);
	pushup(p);
}

然后就是区间求和和最值了，首先假设我们要找的区间为 \([l,r]\)，当前所遍历到的区间为 \([x,y]\)，如果这两个区间八竿子打不着（没有相交）就可以直接跳过了（看情况，求和返回 \(0\)，求最值返回一个很大或很小的数），如果 \([l,r]\) 完全包含 \([x,y]\)，那么直接返回被包含的区间数据，反正都要求了先把部分搞出来在搞全部也可以，如果有相交的地方就接着遍历左右儿子，总有整个区间都被包含的，时间复杂度又双叕叕是 \(O(\log(n))\)。

1
2
3
4
5
6
int getsum(int p,int s,int t){
	if(t<tree[p].l||s>tree[p].r)return 0;
	if(s<=tree[p].l&&tree[p].r<=t)return tree[p].val;
	return getsum(p<<1,s,t)+getsum(p<<1|1,s,t);
    //求最值：return max/min(getsum(p<<1,s,t),getsum(p<<1|1,s,t));
}

某邪恶的何老板：都这样了，那我不让你去求区间数据，让你求修改完的单点数据怎么办？这还不简单，从根节点开始一直二分遍历自己的所有儿子，总有一个儿子是只包含这一个点的，时间复杂度……传奇 \(O(\log(n))\)。

1
2
3
4
5
int getval(int p,int k){
	if(tree[p].l==tree[p].r)return tree[p].val;
	if(k<=tree[p<<1].r)return getval(p<<1,k);
	if(k>=tree[p<<1|1].l)return getval(p<<1|1,k);
}

接下来就该是区间修改了: - 在区间修改时，显然不能暴力地修改每个叶子，那样效率很低。 - 为此，引入延迟标记（又称为懒标记或者 lazy），记录一些区间修改的信息。 - 当递归至一个被完全包含的区间时，在这个区间上打一个延迟标记，记录这个区间中的每个数都需要被加上某个数，然后直接修改该结点的区间和并返回，不再向下递归（省时）。 - 当新访问到一个结点时，先将延迟标记下放到子结点结点，然后再进行递归。

简而言之：
如果需要对一个区间中每一个叶结点进行操作，我们不妨先别忙着操作，而是在所有大区间上做一个标记，下一次遇到或要用到时，再进行处理（标记传递）。

具体的例子可以通过下面的图片来了解一下。
2.PNG

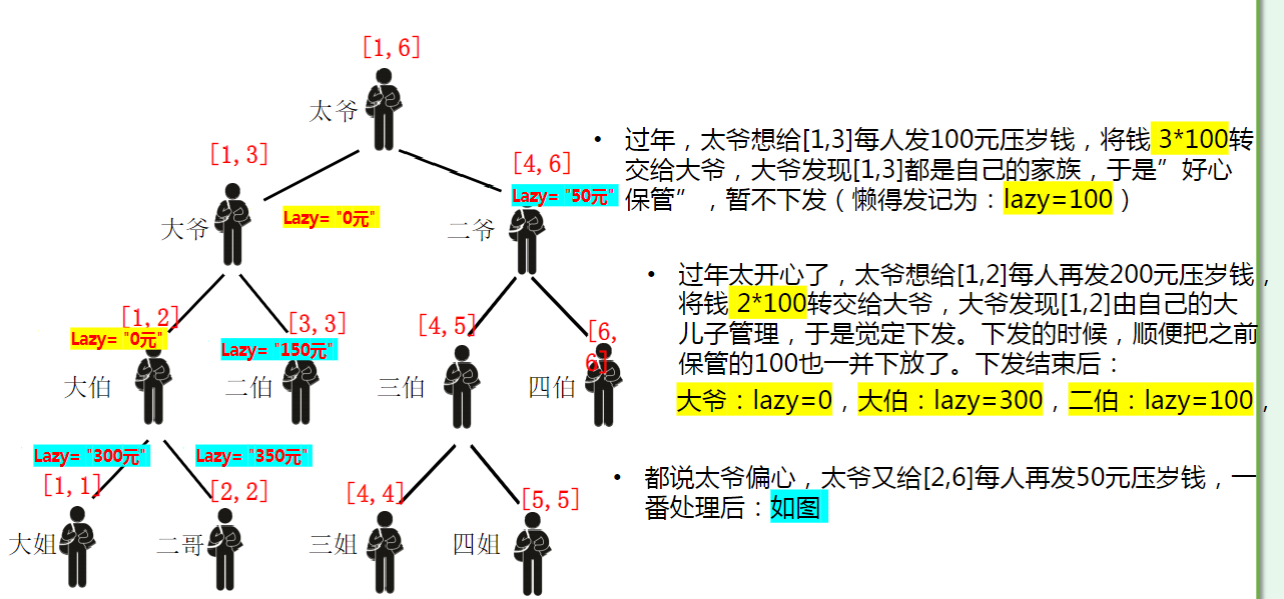
但是懒标记有的时候可能修改完了都还没有分下去，于是我们再求答案时也需要再下放一次懒标记。

至于代码部分，区间修改的代码相较于单点修改差不多，就是在更改这一节点是也一起更改懒标记，更新懒标记直接二分模拟，下发懒标记同样模拟，但要注意，只有在这个懒标记的值不为 \(0\) 时才能下发，时间复杂度……\(O(\log(n))\) 得了 MVP。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void maketag(int p,int len,int x){
	tree[p].lazy+=x;
	tree[p].val+=x;
}
void pushdown(int p){
	int M=tree[p].r+tree[p].l>>1;
	maketag(p<<1,M-tree[p].l+1,tree[p].lazy);
	maketag(p<<1|1,tree[p].r-M,tree[p].lazy);
	tree[p].lazy=0;
}
void tag(int u){
	if(tree[u].lazy){
		int d=tree[u].lazy;
		tree[u].lazy=0;
		tree[u<<1].lazy+=d;
		tree[u<<1].val+=d;
		tree[u<<1|1].lazy+=d;
		tree[u<<1|1].val+=d;
	}
}
void add(int p,int x,int y,int d){
	if(x<=tree[p].l && tree[p].r<=y){
		tree[p].val+=d;
		tree[p].lazy+=d;
		return;
	}
	tag(p);
	int mid=tree[p].l+tree[p].r>>1;
	if(x<=mid) add(p<<1,x,y,d);
	if(y>mid) add(p<<1|1,x,y,d);
	pushup(p);
}

Part 3.动态开点线段树

先讲一个故事：有一天，我正在亲亲苦苦的刷线段树的题，看到一个题我觉得像模版就应该不难，然后数组 \(10^5\) 不想改了，正常写完交上去硬控我三分钟。

logo

后来一看数据……

logo

\(10^9\) 的数据空间太大了，肯定不能用普通线段树去做，而这个问题有做多只会有 \(5 \times 10^5\) 的操作次数。因此，动态开点线段树就可以完成这个问题。

首先朴素线段树的建树是每一个节点都要建，这样很费空间，动态开点线段树是要用到的节点才建树，举个例子，当前遍历到了节点 \(x\)，则 \(x\) 的所有祖宗节点都需要建，其他点就不用。

翻译成人话：线段树动态开点的意思是一开始不用建立树，当我们在进行操作过程中，发现需要走到一个节点时，如果这个节点还没建立，我们才建立这个节点。

动态开点的作用是节约空间，避免离散化，时间复杂度同朴素线段树。

下图就是一个例子：
3.PNG

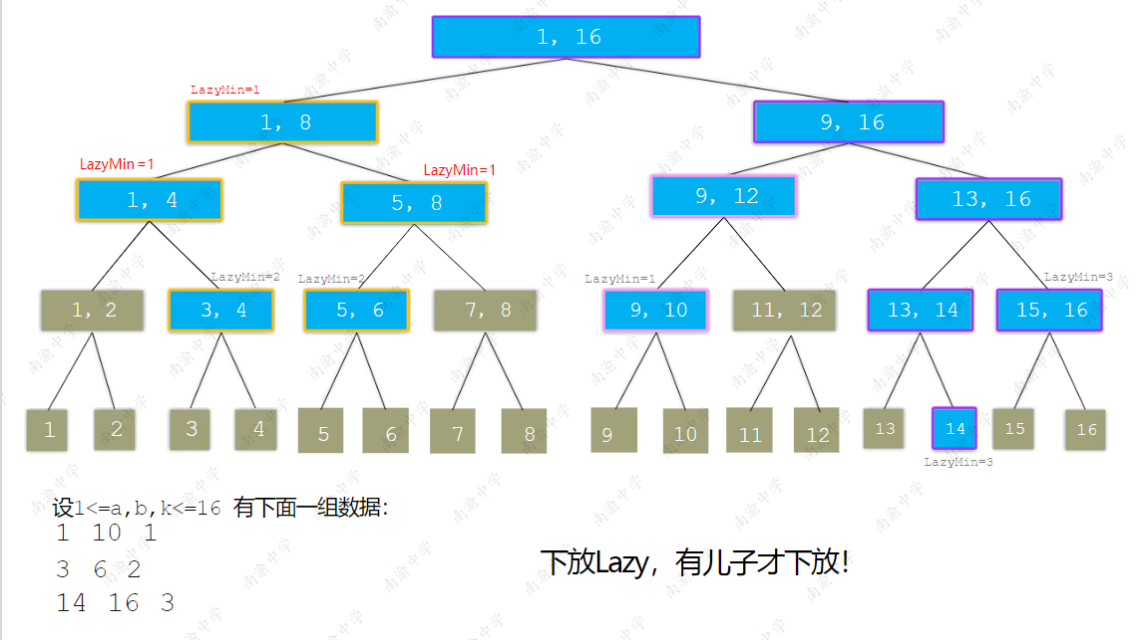
至于代码部分，由于每次构建的节点不像线段树一样有一个固定的编号，因此需要自己设立一个变量来记录当前遍历到的节点的编号，其余部分同朴素线段树，本文用 \(tot\) 来表示节点的编号，注意：\(tot\) 需要初始化为 \(1\)，首个需自行建立的节点计算时编号为 \(2\) 编号为 \(1\) 的节点为根节点。

细节：使用动态开点线段树是为了节省空间，因此数组无需开四倍。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
const int maxn=5e5+5;
const int MAXN=1e9;
int n,m,k,ans,tot=1,ls[maxn*4],rs[maxn*4],lazy[maxn*4];
void add(int p,int l,int r,int x,int y,int d){
	if(x<=l&&r<=y){
		lazy[p]=max(lazy[p],d);
		return;
	}
	int mid=(l+r)>>1;
	if(x<=mid){
		if(ls[p]==0)ls[p]=++tot;
		add(ls[p],l,mid,x,y,d);
	}
	if(mid<y){
		if(rs[p]==0)rs[p]=++tot;
		add(rs[p],mid+1,r,x,y,d);
	}
}
void putdown(int p){
	if(ls[p])lazy[ls[p]]=max(lazy[ls[p]],lazy[p]);
	if(rs[p])lazy[rs[p]]=max(lazy[rs[p]],lazy[p]);
}
int getans(int p,int l,int r){
	putdown(p);
	if(l==r)return lazy[p];
	int sum=0;
	int mid=(l+r)>>1;
	if(ls[p])sum+=getans(ls[p],l,mid);
	else sum+=lazy[p]*(mid-l+1);
	if(rs[p])sum+=getans(rs[p],mid+1,r);
	else sum+=lazy[p]*(r-mid);
	return sum;//依旧以求和为例
}

完结撒花！

inf.鸣谢

感谢 lijing2020 的教学与精神支持！
感谢 Huchangzhi 的课件记录！